solve the assignment problem represented by the following matrix

Procedure, Example Solved Problem | Operations Research - Solution of assignment problems (Hungarian Method) | 12th Business Maths and Statistics : Chapter 10 : Operations Research

Chapter: 12th business maths and statistics : chapter 10 : operations research.

Solution of assignment problems (Hungarian Method)

First check whether the number of rows is equal to the numbers of columns, if it is so, the assignment problem is said to be balanced.

Step :1 Choose the least element in each row and subtract it from all the elements of that row.

Step :2 Choose the least element in each column and subtract it from all the elements of that column. Step 2 has to be performed from the table obtained in step 1.

Step:3 Check whether there is atleast one zero in each row and each column and make an assignment as follows.

Step :4 If each row and each column contains exactly one assignment, then the solution is optimal.

Example 10.7

Solve the following assignment problem. Cell values represent cost of assigning job A, B, C and D to the machines I, II, III and IV.

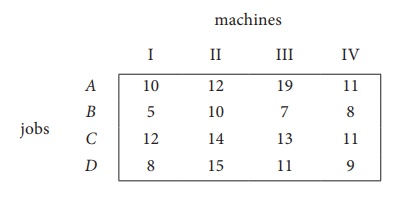
Here the number of rows and columns are equal.

∴ The given assignment problem is balanced. Now let us find the solution.

Step 1: Select a smallest element in each row and subtract this from all the elements in its row.

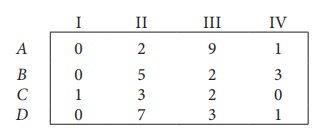
Look for atleast one zero in each row and each column.Otherwise go to step 2.

Step 2: Select the smallest element in each column and subtract this from all the elements in its column.

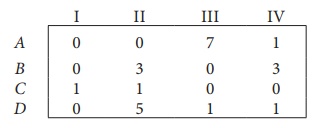
Since each row and column contains atleast one zero, assignments can be made.

Step 3 (Assignment):

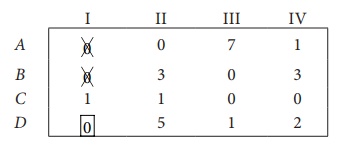
Thus all the four assignments have been made. The optimal assignment schedule and total cost is

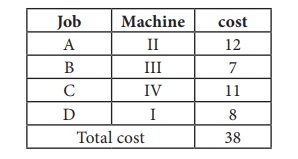
The optimal assignment (minimum) cost

Example 10.8

Consider the problem of assigning five jobs to five persons. The assignment costs are given as follows. Determine the optimum assignment schedule.

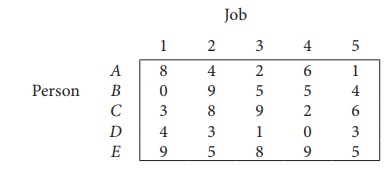
∴ The given assignment problem is balanced.

Now let us find the solution.

The cost matrix of the given assignment problem is

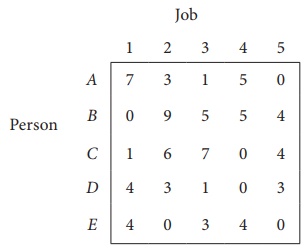
Column 3 contains no zero. Go to Step 2.

Thus all the five assignments have been made. The Optimal assignment schedule and total cost is

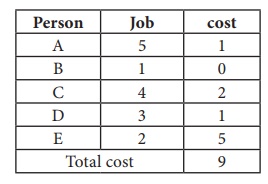
The optimal assignment (minimum) cost = ` 9

Example 10.9

Solve the following assignment problem.

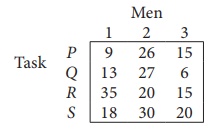
Since the number of columns is less than the number of rows, given assignment problem is unbalanced one. To balance it , introduce a dummy column with all the entries zero. The revised assignment problem is

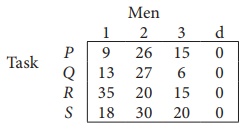
Here only 3 tasks can be assigned to 3 men.

Step 1: is not necessary, since each row contains zero entry. Go to Step 2.

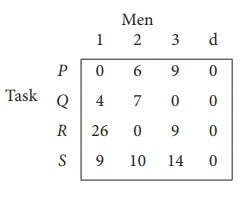
Step 3 (Assignment) :

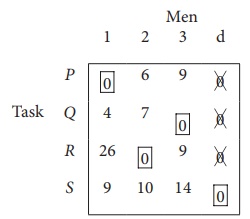
Since each row and each columncontains exactly one assignment,all the three men have been assigned a task. But task S is not assigned to any Man. The optimal assignment schedule and total cost is

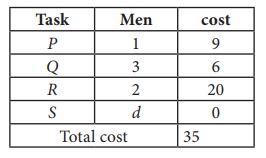
The optimal assignment (minimum) cost = ₹ 35

Related Topics

Privacy Policy , Terms and Conditions , DMCA Policy and Compliant

Copyright © 2018-2023 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.

Index     Assignment problem     Hungarian algorithm     Solve online    

Solve an assignment problem online

Fill in the cost matrix of an assignment problem and click on 'Solve'. The optimal assignment will be determined and a step by step explanation of the hungarian algorithm will be given.

Fill in the cost matrix ( random cost matrix ):

Don't show the steps of the Hungarian algorithm Maximize the total cost

HungarianAlgorithm.com © 2013-2024

• Practice Mathematical Algorithm
• Mathematical Algorithms
• Pythagorean Triplet
• Fibonacci Number
• Euclidean Algorithm
• LCM of Array
• GCD of Array
• Binomial Coefficient
• Catalan Numbers
• Sieve of Eratosthenes
• Euler Totient Function
• Modular Exponentiation
• Modular Multiplicative Inverse
• Stein's Algorithm
• Juggler Sequence
• Chinese Remainder Theorem
• Quiz on Fibonacci Numbers

Hungarian Algorithm for Assignment Problem | Set 1 (Introduction)

• For each row of the matrix, find the smallest element and subtract it from every element in its row.
• Do the same (as step 1) for all columns.
• Cover all zeros in the matrix using minimum number of horizontal and vertical lines.
• Test for Optimality: If the minimum number of covering lines is n, an optimal assignment is possible and we are finished. Else if lines are lesser than n, we haven’t found the optimal assignment, and must proceed to step 5.
• Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.

Try it before moving to see the solution

Explanation for above simple example:

  An example that doesn’t lead to optimal value in first attempt: In the above example, the first check for optimality did give us solution. What if we the number covering lines is less than n.

Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3).

Space complexity :   O(n^2), where n is the number of workers and jobs. This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional arrays of size n to store the labels, matches, and auxiliary information needed for the algorithm.

In the next post, we will be discussing implementation of the above algorithm. The implementation requires more steps as we need to find minimum number of lines to cover all 0’s using a program. References: http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf https://www.youtube.com/watch?v=dQDZNHwuuOY

Similar Reads

• Hungarian Algorithm for Assignment Problem | Set 1 (Introduction) Let there be n agents and n tasks. Any agent can be assigned to perform any task, incurring some cost that may vary depending on the agent-task assignment. It is required to perform all tasks by assigning exactly one agent to each task and exactly one task to each agent in such a way that the total 15+ min read
• Hungarian Algorithm for Assignment Problem | Set 2 (Implementation) Given a 2D array, arr of size N*N where arr[i][j] denotes the cost to complete the jth job by the ith worker. Any worker can be assigned to perform any job. The task is to assign the jobs such that exactly one worker can perform exactly one job in such a way that the total cost of the assignment is 7 min read
• Introduction to Exact Cover Problem and Algorithm X If you have ever tried to create a program for solving Sudoku, you might have come across the Exact Cover problem. In this article, we will discuss what is the exact cover problem and an algorithm “Algorithm X” proposed by Donald Knuth to solve this problem. Given a collection S of subsets of set X, 6 min read
• Greedy Approximate Algorithm for Set Cover Problem Given a universe U of n elements, a collection of subsets of U say S = {S1, S2...,Sm} where every subset Si has an associated cost. Find a minimum cost subcollection of S that covers all elements of U. Example: U = {1,2,3,4,5} S = {S1,S2,S3} S1 = {4,1,3}, Cost(S1) = 5 S2 = {2,5}, Cost(S2) = 10 S3 = 6 min read
• Job Assignment Problem using Branch And Bound Let there be N workers and N jobs. Any worker can be assigned to perform any job, incurring some cost that may vary depending on the work-job assignment. It is required to perform all jobs by assigning exactly one worker to each job and exactly one job to each agent in such a way that the total cost 15+ min read
• Top 50 Graph Coding Problems for Interviews Here is the collection of the Top 50 list of frequently asked interview questions on Graph. Problems in this Article are divided into three Levels so that readers can practice according to the difficulty level step by step. Level 1Problems Solve Print Adjacency ListSolveBFS of GraphSolveDFS of Graph 2 min read
• Channel Assignment Problem There are M transmitter and N receiver stations. Given a matrix that keeps track of the number of packets to be transmitted from a given transmitter to a receiver. If the (i; j)-th entry of the matrix is k, it means at that time the station i has k packets for transmission to station j. During a tim 14 min read
• Chocolate Distribution Problem | Set 2 Given an array A[] consisting of N integers, where each value represents the marks of the ith student, the task is to find the minimum number of chocolates required to be distributed such that: Each student should be awarded with at least one chocolateA student with higher marks should be awarded mo 15+ min read
• Microsoft Interview Experience | Set 140 (On-Campus For Internship) Written Test: 75 minutes online round (Cocubes) in which 3 simple questions were asked. A pool of questions was there and each person will get random questions in each difficulty level. CGPA cutoff was 7. Nearly, 45 people appeared for the test. Given an array of penalties, an array of car numbers a 5 min read
• Flipkart Interview Experience | Set 44 (On-campus for SDE-1) Round 1: Coding Round - 90 minutes - Hackerrank Problem 1 : Given an array of N integers. Find number of sub-arrays with M number of odd integers. Problem 2 : N gears were given each with their own cost ci and radius ri. One extra gear was also given with radius r1. A distance d was given and we had 4 min read
• Maximize score by matching element with prediction and K switch are allowed Given an array arr[] of size N, with values either 1, 2, or 3. Traverse the array from left to right and before traversal predict one number from 1, 2, or 3, if arr[i] is matched with the prediction score will be increased by 1. The prediction can be switched at most K times. Find the maximum score 12 min read
• Possible arrangement of persons waiting to sit in a hall Given an integer N, a binary string S and an array W[]. S denotes the sequence of N * 2 persons entering the hall, where 0 denotes a boy and 1 denotes a girl. W[] denotes the width of seats in each row, where each row consists of exactly 2 seats. The task is to find a possible arrangement of the per 10 min read
• Goldman Sachs Interview Experience | Set 31 (For Internship) Goldman Sachs These are the CS questions asked in the written round of GS in this year's campus internship. There are 36 horses. We have to find out the fastest 3 horses. In one race, maximum 6 horses can run. How many races are required in minimum to get the result without using a stopwatch? We can 4 min read
• Travelling Salesman Problem using Hungarian method A travelling salesman plans to visit N cities in such a way that he visits each city exactly once and return to the city from where he started. The distance between City i and City j is Cij. Find the shortest tour he can take. Note: Travelling from City i to City i is not possible and Cij may not be 5 min read
• Intuit Interview | Set 8 (On-Campus) Intuit came to our college campus for placements. Shortlisted 13 students after written and then selected 4 students for Full Time Job. There were 3 coding questions and 21 (apti+puzzles) to be done in 90 minutes. Apti n puzzle questions were 5 marks each and coding questions were 100 marks each. On 5 min read
• Maximum possible size of subset following the given constraints Given an array arr[] of size n, the task is to find the maximum possible size x of a subset such that there are exactly two subsets of the same size that should follow the below constraints: The first subset should consist of distinct elements (i.e., all elements in the first subset are unique) and 10 min read
• Top 50 Dynamic Programming Coding Problems for Interviews Here is the collection of the Top 50 list of frequently asked interview questions on Dynamic Programming. Problems in this Article are divided into three Levels so that readers can practice according to the difficulty level step by step. Level 1: Dynamic Programming Coding Problems for InterviewsPro 2 min read
• Directi Interview | Set 12 (On-Campus) Recently DirectI visited our campus for placements for three profiles - 1. Platform Engineer 2. Applications Engineer 3. Operations Engineer This process is for the first two profiles, I did not apply for Operations. Round 1: Online coding round (263 applicants) Q1. Given cost C[i] and calorie conte 4 min read
• Maximize count of indices with same element by pairing rows from given Matrices Given two 2D binary arrays, a[][] and b[][] both of size M*N, the task is to pair each row in the array a[][] with any row in the array b[][] such that the total score can be maximized and the score for each pair is calculated as the total indexes at which values of both rows are identical. Note: Ea 15+ min read
• Mathematical

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Operations Research

Lesson 9. SOLUTION OF ASSIGNMENT PROBLEM

Current course

22 February - 28 February

1 March - 7 March

8 March - 14 March

15 March - 21 March

22 March - 28 March

29 March - 4 April

5 April - 11 April

12 April - 18 April

19 April - 25 April

26 April - 2 May